Home

You can look at a geared driveline as 1 'body', with different rotational velocity at the front and rear.

THE PROBLEM

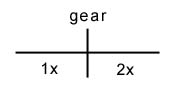You're simulating the driveline. A rod comes in at the gearbox, and a rod comes out rotating twice as fast. You know you can deal with this entire system using just a single (rotational) inertia. Suppose the front rod is 1kg, and the rear one is 1kg. What would be the effective inertia for this, if we only want to use the rotational velocity of the first rod (which we call 'w1')?

THE THOUGHT

At first glance, you might think that as the 2nd rod rotates twice as fast, you have twice as much inertia to deal with, so 'I_effective=I_rod1+2*I_rod2, and as I_rod2=I_rod1, I_effective=3*I_rod1' would spring to mind. Do not use this formula though, but read on.
You still want to have the formula, since it is easier to see the system as just 1 rotating mass, and calculate w2=2*w1 after solving the equation for the entire system.

THE CHECK

As with all programming, it is often possible to take 2 or more routes to come up with the same solution. For Newtonian physics, this is LaGrangian physics (which I haven't actually studied much yet). Basically, it writes the same equations using energy. We use energy to check whether the above formula really makes sense.

As you probably know, the kinetic energy of a mass is KE=1/2*m*v^2. A little less known but equally true is the rotational kinetic energy (as long as we're not doing space sims, which need to deal with Einsteins theory of relativity); RKE=1/2*I*w^2, where I is the inertia (this is actually a 3x3 tensor, but with the rods we'll just use 1 scalar, giving the inertia of the rotation around its natural axis), and 'w' is the angular (rotation) speed. We plug in the above formulae and get:

RKE_total = 1/2*I_rod1*w1^2 + 1/2*I_rod2*w2^2

We know that the rods have equal weight, so I_rod1=I_rod2. And, through the gearing, w2=2*w1. This makes for:

RKE_total = 1/2*I_rod1*w1^2 + 1/2*I_rod1*(2*w1)^2

so

RKE_total = (1+4)*(1/2*I_rod1*w1^2)

although the formula first presented would state:

RKE_effective=1/2*I_effective*w1^2

so

RKE_effective=1/2*(3*I_rod1)*w1^2 = (1+2)*(1/2*I_rod1*w1^2)

This is conflicting, and the first intuitive effective inertia formula is bad (as you get conflicting amounts of energy, which is ofcourse not possible).

THE SOLUTION

Given a good sense of intuition, the energy formula RKE_total from above gives the idea that the effective inertia should be calculated as this:

I_effective = I_rod1+(gearRatio^2)*I_rod2, and I_rod1=I_rod2 (in this case)

Where 'gearRatio' was 2 in our example. Checking this with the RKE formula gives us the correct:

RKE_effective = 1/2*I_effective*w1^2 = (1+4)*(1/2*I_rod1*w1^2)

(note you only have to calculate w2 later on by noting that w2=gearRatio*w1)

GEARING MULTIPLE COMPONENTS

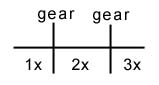In the same way you can expand this to a 3-way system. Here, the system is geared 1:2:3, so the 3rd rod rotates at 2x3 = 6 times the speed of rod1.

You might wonder whether you should take I_eff=I_1+(2^2)*I_2+(3^2)*I_3 or perhaps use (2*3)^2*I_3 even. Write down the energy equation, RKE:

I_1=I_2=I_3, w2=2*w1, w3=6*w1

RKE=1/2*I_1*w1^2+1/2*I_2*w2^2+1/2*I_3*w3^2

so

RKE=1/2*I_1*w1^2 + 1/2*I_1*(2*w1)^2 + 1/2*I_3*(6*w1)^2

ending up at

RKE=(1+4+36)*I_1*w1^2

So you see that the last term in the first factor is 36, which is 6^2. So the general formula becomes:

I_effective = I_1 + (gearRatio1^2)*I_2 + ((gearRatio2*gearRatio1)^2)*I_3

and this would lead a conclusion that with 4 components you'd get:

I_effective = I_1 + (gearRatio1^2)*I_2 + ((gearRatio2*gearRatio1)^2)*I_3 + ((gearRatio3*gearRatio2*gearRatio1)^2)*I_4

Where ofcourse in this example, gearRatio1 was 2, and gearRatio2 was 3.

REFERENCES

The idea from the need to square the ratio's comes from Gillespie's book 'Fundamentals of Vehicle Dynamics'; see the references page.

(last updated November 13, 2012 )